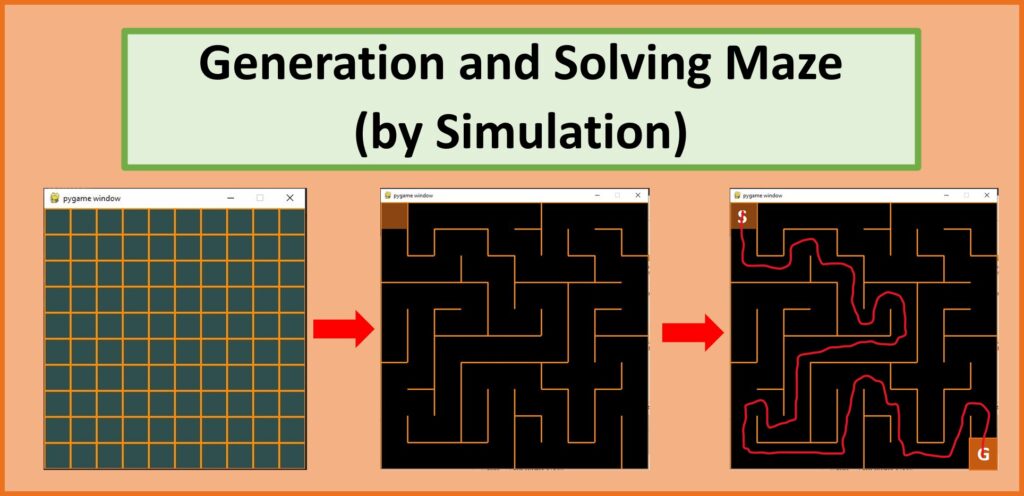
ที่มาและปัญหา : โครงการนี้เป็นโครงการที่ส่งหุ่นยนต์ออกไปเก็บข้อมูลในเขาวงกต และสามารถเลือกเส้นทางจากจุดเริ่มต้นไปยังทางออกที่เร็วที่สุดได้
วัตถุประสงค์ : สามารถเขียนอัลกอริทึมในการเก็บแผนที่ของเขาวงกต และหาทางออกจากเขาวงกตได้
สมมุติฐาน : หุ่นยนต์สามารถเดินเก็บข้อมูลของเขาวงกต และหาเส้นทางที่เร็วที่สุดในการออกจากเขาวงกต
ขอบเขตการศึกษา : Program Visual Studio
ประโยชน์ที่คาดว่าจะได้รับ : การเรียนรู้ concept พื้นฐานของการเขียนโปรแกรมและ data structure เบื้องต้น
ผลงานวิจัยและทฤษฎีที่เกี่ยวข้อง
Dept First search (DFS)
การค้นหาแบบลึกก่อน(Depth first search) (DFS) เป็นการค้นหาที่กําหนดทิศทางจากรูปของโครงสร้างต้นไม้ ที่เริ่มต้นจากโหนดราก(Root node) ที่อยู่บนสุด แล้วเดินลงมาให้ลึกที่สุด เมื่อถึงโหนดล่างสุด(Terminal node) ให้ย้อนขึ้นมาที่จุดสูงสุดของกิ่งเดี่ยวกันที่มีกิ่งแยกและยังไม่ได้เดินผ่าน แล้วเริ่มเดินลงจนถึงโหนดลึกสุดอีก ทําเช่นนี้สลับไปเรื่อยจนพบโหนดที่ต้องการหาหรือสํารวจครบทุกโหนดแล้วตามรูปที่ 1 การค้นหาแบบลึกก่อนจะมีลําดับการเดิน ตามโหนดดังตัวอักษรที่กํากับไว้ในแต่ละโหนด.
โดย DFS จะมีการค้นหา สามวิธีคือ
• Preordering คือรายการของการจุดที่เป็นจุดเริ่มในการค้นหาแบบลึกก่อน. นี้เป็นวิธีที่กะทัดรัดและเป็นธรรมชาติในการอธิบายความคืบหน้าของการค้นหา การPreordering ของต้นไม้ได้แสดงออกมาใน Polish notation.
• Postordering คือรายการของการจุดที่เป็นจุดสุดท้ายหรือครั้งล่าสุดในการค้นหาแบบลึกก่อน. Postordering ของ ต้นไม้ได้แสดงออกมาใน reverse Polish notation.
• Postordering reverse เป็น reverse ของ postordering เช่นรายการจุดตามลำดับตรงข้ามของการเข้าชมครั้งล่าสุด. เมื่อเริ่มค้นหาในกราฟแบบต้นไม้, postordering reverse จะเหมือนกับ preordering แต่โดยทั่วไปจะแตกต่างกันเมื่อค้นหากราฟธรรมดา. เช่นการค้นหากราฟโดยตรง
รูปที่ 1 การค้นหาแบบ Depth first search (DFS)
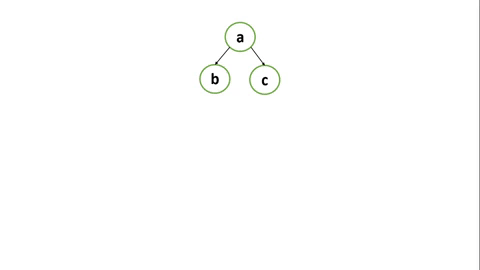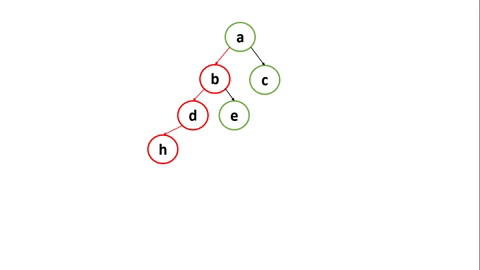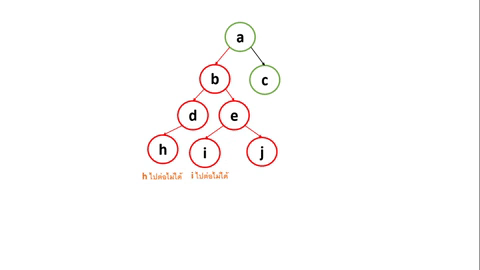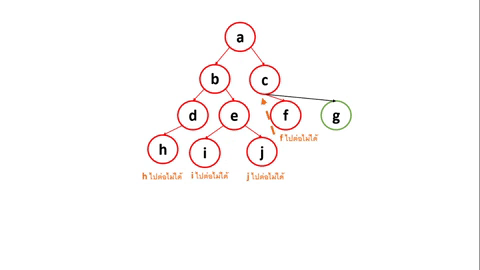
ซึ่งการค้นหาแบบ DFS เป็นการค้นหาเชิงลึก ซึ่งจะสุ่มไปให้สุดทางก่อนจะกลับมาที่ตำแหน่งจุดสูงสุดที่มีการแยกกัน สามารถอธิบายได้ตามรูปที่ 1 ดังนี้
- เริ่มต้นที่ node a มีทางแยก 2 ทางคือ b และ c
- DFS จะสุ่มเลือกเส้นทาง โดยเริ่มต้นที่ node b (วิธีแบบ Preordering)
- node b มีทางแยก คือ d และ e
- DFS จะสุ่มเลือกที่เส้นทาง node d (วิธีแบบ Preordering)
- node d มี node ที่เชื่อมต่อเพียง h ดังนั้นเส้นทางจึงไปต่อไม่ได้ (วิธีแบบ Postordering)
- DFS ย้อนกลับมายังตำแหน่ง node b (วิธีแบบ Postordering reverse) ซึ่งมีทางแยก คือ d และ e โดย d จะถูกทำเครื่องหมายว่าตำแหน่งนี้ไปมาแล้ว ดังนั้นตำแหน่งที่จะไปต่อคือ node e
- node e มี ทางแยกคือ i และ j
- DFS จะสุ่มเลือกที่เส้นทาง node i (วิธีแบบ Preordering)
- node i ไปต่อไม่ได้แล้ว จึงย้อนกลับมาที่ node e ใหม่
- DFS เลือกเส้นทางที่เหลือ คือ node j
- node j ไปต่อไม่ได้ (วิธีแบบ Postordering) จึงย้อนกลับมา ซึ่งคราวนี้จะย้อนกลับมายังตำแหน่งทางแยกก่อนหน้าที่ยังเหลือทางที่ยังไม่ได้ไป ก็คือ node c (วิธีแบบ Postordering reverse)
- node c มีทางแยกคือ f และ g
- DFS จะสุ่มเลือกที่เส้นทาง node f ก่อน (วิธีแบบ Preordering)
- node f ไปต่อไม่ได้ (วิธีแบบ Postordering) ย้อนมาที่ node c อีกครั้ง (วิธีแบบ Postordering reverse)
- DFS จะสุ่มเลือกเส้นทางที่เหลือ คือ node g ซึ่งไปต่อไม่ได้ (วิธีแบบ Postordering) และจบการทำงาน
Breadth-First search (BFS)
การค้นหาในแนวกว้างก่อน (Breadth-First search) (ฺBFS) เป็นขั้นตอนการหากราฟทั้งหมด ที่โหนดเริ่มต้น (Root) และทำการสำรวจโหนดของเพื่อนบ้าน การค้นหาแบบกว้างก่อนเป็นการกําหนดทิศทางการค้นหาแบบที่ละระดับของโครงสร้างต้นไม้โดยเริ่มจากโหนดราก(ระดับที่ 0) แล้วลงมาระดับที่ 1 จากซ้ายไปขวา เมื่อเสร็จระดับที่ 1 ไประดับที่ 2 จากซ้ายไปขวาเช่นกัน ทําเช่นนี้เรื่อย ๆ จนพบโหนดที่ต้องการตามรูปที่ 2 ลําดับการเดินทางของโหนดเป็นไปตามอักษรที่กํากับไว้บนโหนด
รูปที่ 2 การค้นหาแบบ ฺBreadth-first search (BFS)
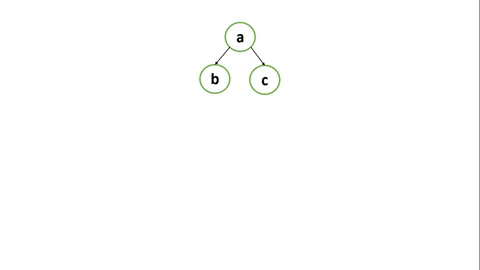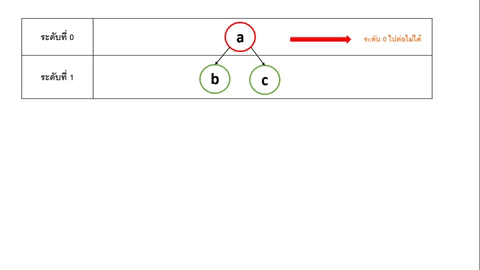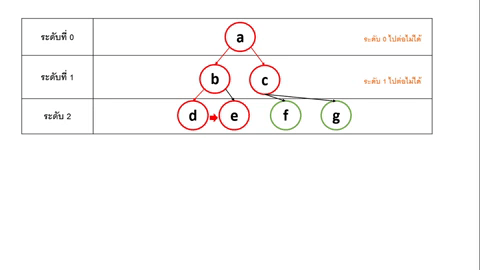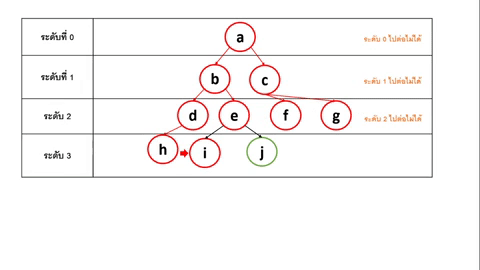
ซึ่งการค้นหาแบบ BFS เป็นการค้นหาแนวกว้าง ซึ่งจะเริ่มต้นสำรวจจากทิศทาง ซ้ายไปขวา โดยเริ่มจาก ระดับที่ 0 และไล่ไปทีล่ะระดับ จนกว่าจะไม่มีโหนดอื่นในระดับถัดไป สามารถอธิบายได้ตามรูปที่ 2
- เริ่มต้นที่ node a ในระดับที่ 0
- เนื่องจาก node a มีแค่ node เดียว ในระดับ 0 จึงไปต่อไม่ได้ จึงไประดับถัดไป
- ในระดับที่ 1 มี node a แยกเส้นทางเป็น b และ c
- BFS จะสำรวจ node b ก่อน และ สำรวจใน node c เป็นลำดับถัดไป
- ในระดับที่ 1 ต่อจาก node c ไปต่อไม่ได้ จึงไประดับถัดไป
- ในระดับที่ 2 มี node b แยกเส้นทางเป็น d กับ e และ node c แยกเส้นทางเป็น f กับ g
- BFS จะสำรวจ node d ก่อน และตามด้วย node e, node f, node g ตามลำดับ
- ในระดับ 2 ต่อจาก node g ไปต่อไม่ได้ จึงไประดับถัดไป
- ในระดับที่ 3 มี node d แยกเส้นทางเป็น h และ node e แยกเป็น i กับ j
- BFS จะสำรวจ node h ก่อน และตามด้วย node i, node j ตามลำดับ
- ในระดับที่ 3 ต่อจาก node j ไปต่อไม่ได้ จึงไประดับถัดไป
- ในระดับถัดไป ไม่มี node จึง จบการทำงาน
ภาพรวมรายละเอียดโดยรวมของระบบ
จากวัตถุประสงค์ที่ต้องการให้เขียนอัลกอริทึมในการเก็บแผนที่ของเขาวงกต และหาทางออกจากเขาวงกตได้
ดังนั้น เป้าหมายในการสร้างโปรเจคชิ้นนี้ จึงมีอยู่ 2 อย่างด้วยกันคือ
- การเก็บแผนที่ในเขาวงกตทั้งหมด : ซึ่งในส่วนนี้ จะใช้ DFS ในการเก็บแผนที่
- การหาเส้นทางในการออกจากเขาวงกต : ซึ่งในส่วนนี้จะใช้ BFS ในการหาเส้นทางเพื่อออกจากเขาวงกต
โดยรูปแบบในการแสดงผล คือการใช้ code python ในการ จำลองการทำงานของอัลกอริทึมทั้งสองออกมา ซึ่งจะออกมาในรูปแบบหน้าต่างโปรแกรม

1. การเก็บแผนที่ในเขาวงกตทั้งหมด
ดังที่ได้กล่าวไปข้างต้น ผู้จัดทำ ได้ใช้วิธีการแบบ DFS หรือ Depth first search ในการเก็บแผนที่เขาวงกต โดยวิธีการทำงาน จะเป็นดังนี้
- เลือก Cell เริ่มต้น และทำเครื่องหมายว่าสำรวจแล้วส่งไปยัง Stack
- ในขณะที่ Stack ไม่ว่าง
- ทำการดึงค่าข้อมูลสุดท้ายของ Cell จาก Stack และทำให้เป็น Cell ปัจจุบัน
- หาก Cell ปัจจุบัน มีพื้นที่ไปต่อที่ยังไม่ได้สำรวจ
- ย้ายเซลล์ปัจจุบันไปที่ Stack
- เลือกเส้นทางที่ยังไม่ได้สำรวจ
- ลบกำแพงระหว่าง Cell ปัจจุบัน และ Cell ที่ถูกเลือก
- ทำเครื่องหมายเซลล์ที่ว่าสำรวจแล้วส่งไปยัง Stack
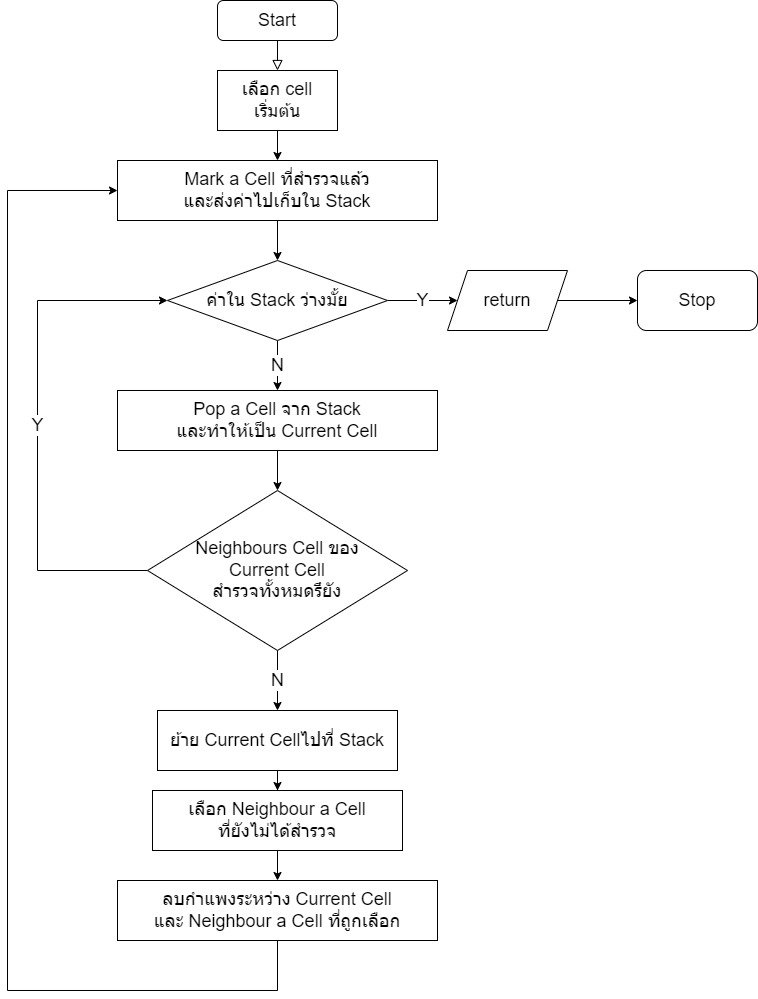
การเก็บแผนที่ โดยใช้อัลกอริทึม DFS
# การสร้างแผนที่จากการใช้ อัลกอริทึม DFS
import pygame
from random import choice
#สร้างขนาดของMaze ที่จะใช้
RES = WIDTH, HEIGHT = 600, 600
TILE = 60
cols, rows = WIDTH // TILE, HEIGHT // TILE
pygame.init()
sc = pygame.display.set_mode(RES)
clock = pygame.time.Clock()
class Cell:
def __init__(self, x, y):
self.x, self.y = x, y
self.walls = {'top': True, 'right': True, 'bottom': True, 'left': True}
self.visited = False
def draw_current_cell(self):
x, y = self.x * TILE, self.y * TILE
pygame.draw.rect(sc, pygame.Color('saddlebrown'), (x + 2, y + 2, TILE - 2, TILE - 2))
def draw(self):
x, y = self.x * TILE, self.y * TILE
if self.visited:
pygame.draw.rect(sc, pygame.Color('black'), (x, y, TILE, TILE))
if self.walls['top']:
pygame.draw.line(sc, pygame.Color('darkorange'), (x, y), (x + TILE, y), 3)
if self.walls['right']:
pygame.draw.line(sc, pygame.Color('darkorange'), (x + TILE, y), (x + TILE, y + TILE), 3)
if self.walls['bottom']:
pygame.draw.line(sc, pygame.Color('darkorange'), (x + TILE, y + TILE), (x , y + TILE), 3)
if self.walls['left']:
pygame.draw.line(sc, pygame.Color('darkorange'), (x, y + TILE), (x, y), 3)
def check_cell(self, x, y):
find_index = lambda x, y: x + y * cols
if x < 0 or x > cols - 1 or y < 0 or y > rows - 1:
return False
return grid_cells[find_index(x, y)]
def check_neighbors(self):
neighbors = []
top = self.check_cell(self.x, self.y - 1)
right = self.check_cell(self.x + 1, self.y)
bottom = self.check_cell(self.x, self.y + 1)
left = self.check_cell(self.x - 1, self.y)
if top and not top.visited:
neighbors.append(top)
if right and not right.visited:
neighbors.append(right)
if bottom and not bottom.visited:
neighbors.append(bottom)
if left and not left.visited:
neighbors.append(left)
return choice(neighbors) if neighbors else False
def remove_walls(current, next):
dx = current.x - next.x
if dx == 1:
current.walls['left'] = False
next.walls['right'] = False
elif dx == -1:
current.walls['right'] = False
next.walls['left'] = False
dy = current.y - next.y
if dy == 1:
current.walls['top'] = False
next.walls['bottom'] = False
elif dy == -1:
current.walls['bottom'] = False
next.walls['top'] = False
grid_cells = [Cell(col, row) for row in range(rows) for col in range(cols)]
current_cell = grid_cells[0]
stack = []
colors, color = [], 40
while True:
sc.fill(pygame.Color('darkslategray'))
for event in pygame.event.get():
if event.type == pygame.QUIT:
exit()
[cell.draw() for cell in grid_cells]
current_cell.visited = True
current_cell.draw_current_cell()
[pygame.draw.rect(sc, colors[i], (cell.x * TILE + 2, cell.y * TILE + 2,
TILE - 4, TILE - 4)) for i, cell in enumerate(stack)]
next_cell = current_cell.check_neighbors()
if next_cell:
next_cell.visited = True
stack.append(current_cell)
colors.append((min(color, 255), 10, 100))
color += 1
remove_walls(current_cell, next_cell)
current_cell = next_cell
elif stack:
current_cell = stack.pop()
pygame.display.flip()
clock.tick(10)
2. การหาเส้นทางในการออกจากเขาวงกต
ดังที่ได้กล่าวไปข้างต้น ผู้จัดทำ ได้ใช้วิธีการแบบ ฺBFS หรือ Breadth first search ในการค้นหาเส้นทางในการออกจากเขาวงกต โดยวิธีการทำงาน จะเป็นดังนี้
- เลือก Cell เริ่มต้น และ Cell เป้าหมาย และเพิ่ม Queue กับ root
- Dequeue Cell จาก Queue
- ในขณะที่ Queue ไม่ว่าง
- ย้ายข้อมูล Cell ไปที่ Queue
- ชี้ ตำแหน่ง root ปัจจุบัน ที่มี Cell อยู่ติดกัน
- ณ ตำแหน่ง root นั้นได้สำรวจ Cell ติดกันหรือไม่
- ถ้า Cell ยังไม่ถูกสำรวจแล้ว
- จะย้ายไปที่ Cell ที่อยู่ติดกัน ใน root นั้น
- ถ้า Cell ถูกสำรวจ จะวางตำแหน่ง Cell มันถูกสำรวจแล้ว
- ถ้า Cell ยังไม่ถูกสำรวจแล้ว
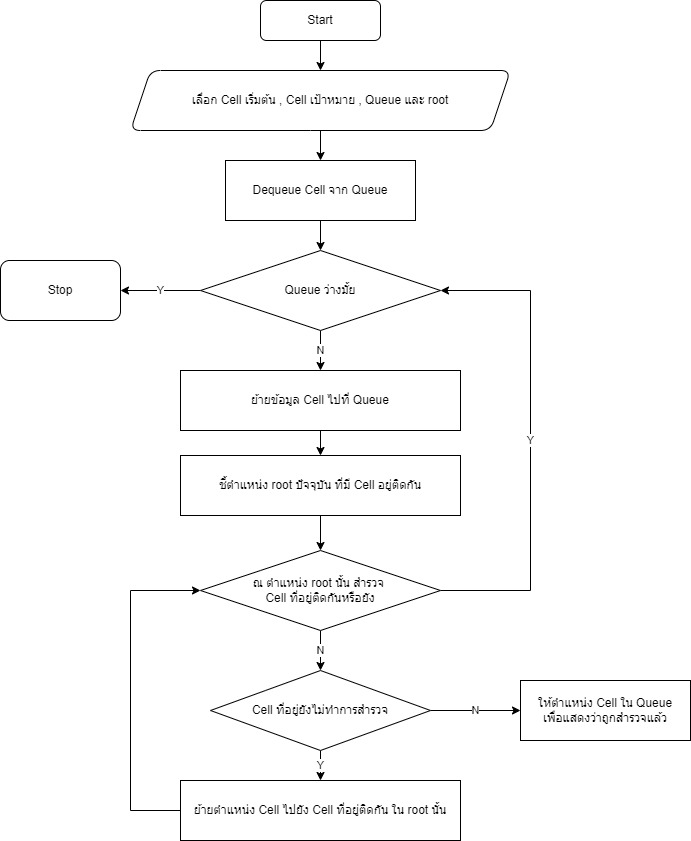
การหาเส้นทางออกจากเขาวงกต โดยใช้อัลกอริทึม BFS
#การหาเส้นทางในการออกจากเขาวงกตด้วย BFS
from pyamaze import maze,agent,textLabel,COLOR
from collections import deque
def BFS(m,start=None):
if start is None:
start=(m.rows,m.cols)
frontier = deque()
frontier.append(start)
bfsPath = {}
explored = [start]
bSearch=[]
while len(frontier)>0:
currCell=frontier.popleft()
if currCell==m._goal:
break
for d in 'ESNW':
if m.maze_map[currCell][d]==True:
if d=='E':
childCell=(currCell[0],currCell[1]+1)
elif d=='W':
childCell=(currCell[0],currCell[1]-1)
elif d=='S':
childCell=(currCell[0]+1,currCell[1])
elif d=='N':
childCell=(currCell[0]-1,currCell[1])
if childCell in explored:
continue
frontier.append(childCell)
explored.append(childCell)
bfsPath[childCell] = currCell
bSearch.append(childCell)
# print(f'{bfsPath}')
fwdPath={}
cell=m._goal
while cell!=(m.rows,m.cols):
fwdPath[bfsPath[cell]]=cell
cell=bfsPath[cell]
return bSearch,bfsPath,fwdPath
if __name__=='__main__':
m=maze(10,10)
# m.CreateMaze(5,4,loopPercent=100)
m.CreateMaze(loopPercent=10,theme='light')
bSearch,bfsPath,fwdPath=BFS(m)
a=agent(m,footprints=True,color=COLOR.blue,shape='square',filled=True)
b=agent(m,footprints=True,color=COLOR.red,shape='square',filled=False)
# c=agent(m,5,4,footprints=True,color=COLOR.cyan,shape='square',filled=True,goal=(m.rows,m.cols))
c=agent(m,1,1,footprints=True,color=COLOR.cyan,shape='square',filled=True,goal=(m.rows,m.cols))
m.tracePath({a:bSearch},delay=100)
m.tracePath({c:bfsPath},delay=100)
m.tracePath({b:fwdPath},delay=100)
m.run()เอกสารอ้างอิง
การค้นหาแบบลึกก่อน
การค้นหาในแนวกว้างก่อน
https://wikkihut.com/breadth-first-traversal/
แนวทางการใช้ DFS และ BFS
- https://www.youtube.com/watch?v=sTRK9mQgYuc
- https://www.youtube.com/watch?v=sTRK9mQgYuc
- https://www.youtube.com/watch?v=Ez7U6jU0q5k
- https://www.youtube.com/watch?v=D14YK-0MtcQ
- https://www.youtube.com/watch?v=abHftC1GU6w
- https://www.youtube.com/watch?v=lyIUnFvYt14
- https://www.youtube.com/watch?v=ZuHW4fS60pc
ผู้จัดทำ
63340700402 นางสาวเมธิณี แสงประดิษฐ์
- ศึกษา ทฤษฎี Depth-First Search และ Breadth-First search
- ออกแบบ และเขียน Algorithm เพื่อเก็บรายละเอียดของแผนที่ และเส้นทางในการออกจากเขาวงกต โดยใช้ ภาษา python ในการเขียน


